Spectral Bin Microphysics Model
はじめに
これまでに、粒径分布とレーダー変数や粒径分布パラメータのレーダー変数による推定といった記事で、主に観測データに関連した話題を扱ってきた。観測データはスナップショットではあるものの、真値に近い状態を示す。一方、時間・空間分解能に制約があるために観測結果がどうしてそうなったのか、という要因の特定には不向きな場合がある。その点を補うものとして、数値モデルによる素過程のシミュレーションや解析が挙げられる。中でも雲微物理過程は、雨や雲を扱う重要な物理過程である。計算コストの観点から、粒径分布は特定の関数で近似されたものが使われることが多い。一方、Spectral bin microphysics (SBM) model は、粒径毎の数濃度等を陽に解くものである。最近では、Hebrew University で開発された Cloud Model (Khain et al. 2004, 2008; HUCM) の spectral (bin) microphysics 部分を他の大気モデルへ移植したものが、利用可能になっている (e.g., Khain et al. 2011; Igel and van den Heever 2017)。本稿では、粒径分布の特徴を把握するためのツールの一つとして、WRF-SBM の利用と簡単な出力結果の描画を試みる。
WRF model
Weather Research and Frecasting Model (WRF) は、主に米国大気研究センターが開発している領域数値気象予報モデルである。WRF のバージョンは、2023年12月22日時点で 4.5.2 が最新版である (参考)。HUCM SBM は mp_physics = 32 or 30 として実装されている。これらは、それぞれ FULL-SBM、FAST-SBM と呼ばれている。前者は計算時間を要するものの物理過程の厳密さを重視したバージョン、後者は前者を特定の現象に対してやや簡略化し計算コストを減少させたバージョンである。バージョン 4.4.1 以降、FAST-SBM のみ利用可能であり、FULL-SBM は利用不可となっている (参考)。ここでは、計算速度よりも物理過程の正確さを重視することを目的とし、FULL-SBM が利用可能なバージョン 4.2.2 を用いることにした (参考)。
動作環境
- Rocky Linux 8.9 x86_64
- GNU compiler version 8.5.0
- NetCDF-C version 4.7.0
- NetCDF-Fortran version 4.5.2
- HDF5 version 1.10.5
- ZLIB version 1.2.11
- WRF version 4.2.2
必要なライブラリは、dnf install した。
コンパイル
export NETCDF=/usr && export HDF5=/usr- 事前に環境変数の指定が必要。
- 場合によっては、
export NETCDF_classic=1も必要。
./configure- 34 番の GNU compiler smpar (OpenMP) を選択。
configure.wrf の LIB_EXTERNAL に -L/usr/lib64 を追記し、コンパイル。
./compile em_quarter_ss
main/ 以下に ideal.exe と wrf.exe が生成されていれば、コンパイル成功。
出力変数の追加
今回は、粒径分布の特徴を把握することを意図し、各 bin の変数を出力できるように修正を施す。出力変数を追加するには、Registry を編集するのが一番簡単。方法は下記。
Registry/registry.sbmの編集ff?i??を出力する。下2桁が bin 番号になっていて、bin 毎に変数が出力される。- 各変数の
h3rusdf=(bdy_interp:dt)の部分をhrusdf=(bdy_interp:dt)にすると良い。- 元の
h3の3は I/O stream 番号 3、つまり Fortran でいうところの出力番号に相当。 - WRF では、主出力ファイルとは別名で変数を出力するオプションがある。
- 詳細はこちらを参照。
- 元の
- 再コンパイル
Registryを変更した場合、反映させるためには再コンパイルが必要。./clean && ./compile em_quarter_ss
定数ファイルの準備
WRF で SBM を実行するには、追加の定数ファイルが必要となる。下記に従い、定数ファイルをダウンロード・展開・配置する。
- こちらから3つのファイルをダウンロードし、
test/em_quarter_ss/以下にそれぞれ展開・配置する。- SBM_input_33.tgz
- SBM_input_43.tgz
- SBM_scatter_amplit.tgz
実行
準備が出来たら、namelist.input を編集し、ideal.exe、wrf.exe の順に実行する。
今回は、ideal case = 2 の supercell 理想化実験を用いる。namelist.input で mp_physics = 32 に変更し、雲微物理過程のみ用いる。計算領域は、mass point で 41x41x40 grid (水平方向 82 km、鉛直方向に 20 km)。モデル上端から 5 km までダンピング層を配置。ideal.exe を実行すると wrfinput_d01 が出力され、その後 wrf.exe を実行すると wrfout_d01_* が出力される。
データの描画
まず、初期プロファイルの input_sounding データを Skew-T LogP plot by MetPy の方法で描画する。ただし、read_fwf の引数に infer_nrows=222 を追加する。理由は、行数のデフォルト値が 100 に制限されているため。

横軸は気温または露点温度 (degree C)、縦軸は気圧 (hPa)。黒実線で気温、青実線で露点温度、橙点線で持ち上げたパーセルの気温をそれぞれ示す、赤色の陰影で示される面積は、持ち上げたパーセルと周辺大気との気温差、すなわち対流有効位置エネルギー (CAPE) である。黒丸印は持ち上げ凝結高度 (LCL) を示す。Skew-T LogP plot by MetPy で示した例よりも赤色の陰影で示される面積が大きく、また、中・上層は乾燥している点も異なる。
次に、WRF の出力結果 wrfout_d01_* を wrf-python により描画する。
import numpy as np
from netCDF4 import Dataset
import matplotlib
import matplotlib.pyplot as plt
from wrf import (to_np, getvar)
# WRF 出力ファイル指定
ncfile = Dataset("wrfout_d01_0001-01-01_00:50:00")
# QRAIN 変数を取得
qr = getvar(ncfile, "QRAIN")
# 描画開始 (xy 断面)
fig = plt.figure(figsize=(8,6))
# 雨水混合比の描画
plt.contourf(to_np(qr[0,15:25,15:25].west_east)+15,
to_np(qr[0,15:25,15:25].south_north)+15,
to_np(qr[0,15:25,15:25]),
10,
cmap=matplotlib.colormaps.get_cmap("jet"))
# カラーバー追加
plt.colorbar(shrink=.98)
# タイトル描画
plt.title("QRAIN (k = "+str(kk)+")")
plt.xlabel('west_east grid number')
plt.ylabel('south_north grid number')
plt.grid()
plt.show()
# 描画開始 (xz 断面)
fig = plt.figure(figsize=(8,6))
# 雨水混合比の描画
plt.contourf(to_np(qr[:15,22,16:23].west_east)+16,
to_np(qr[:15,22,16:23].bottom_top),
to_np(qr[:15,22,16:23]),
10,
cmap=matplotlib.colormaps.get_cmap("jet"))
# カラーバー追加
plt.colorbar(shrink=.98)
# タイトル描画
plt.title(qr.description + " (" + qr.units + ")")
plt.xlabel('west_east grid number')
plt.ylabel('bottom_top grid number')
plt.grid()
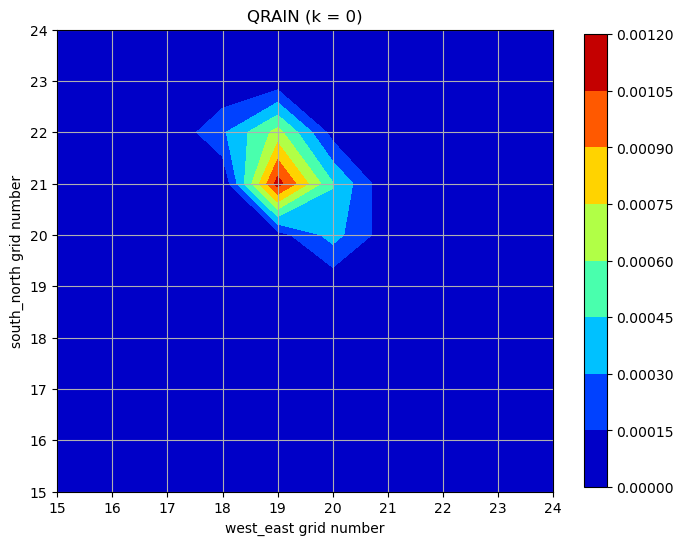
plt.show()計算開始 50 分後の雨水混合比の水平分布。グリッド位置 (19,21) で雨水混合比の極大値が計算されている。
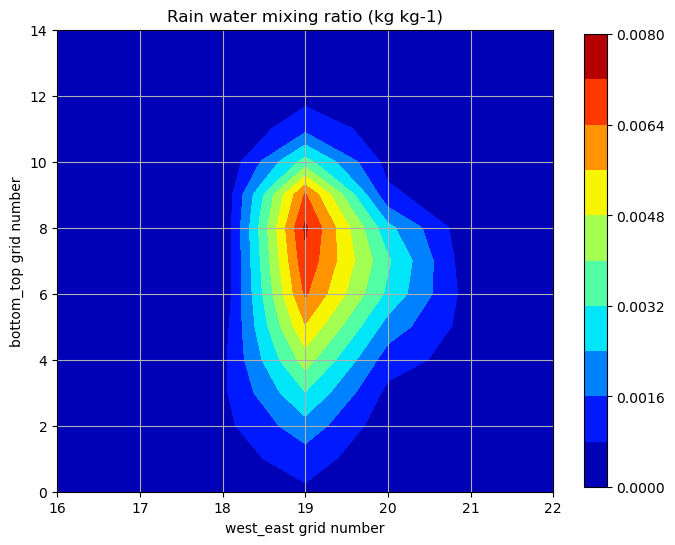
雨水混合比の y = 22 における x-z 断面。地上付近に計算されていた雨水混合比は、鉛直方向には一様ではなく高度とともに値が変化している。
以後、QRAIN の極大値が計算されていたグリッド近傍の (19,22) に着目する。
出力結果から粒径分布を計算
方針は下記の通り。
- 定数ファイル読み込み
- 粒径 (
bulkradii.asc_s_0_03_0_9) - 密度 (
bulkdens.asc_s_0_03_0_9) - 質量 (
masses.asc)
- 粒径 (
- WRF の出力結果読み込み
wrf-pythonでff1i01-ff1i33を読み込み。xarrayのdataarrayをまとめてdatasetにする。- 粒径分布の計算し、粒径分布の描画。今回は、特定 grid の粒径分布を鉛直方向 4 grid 分を図示。
ソースコードは下記。
import numpy as np
from netCDF4 import Dataset
import matplotlib
import matplotlib.pyplot as plt
from wrf import getvar
# 粒径 (半径) [unit: cm] 定数データ読み込み
# index とカテゴリの対応は下記。
# 0: cloud + rain
# 1: ice/columns
# 2: ice/plates
# 3: ice/dendrites
# 4: snow
# 5: graupel
# 6: hail
bulkradii = [[0] * 33 for i in range(7)]
with open("bulkradii.asc_s_0_03_0_9") as f1:
k = 0
j = 0
for line in f1:
records = line.rstrip('\n')
columns = records.split(' ')[:]
for i in range(len(columns)):
if (columns[i] != ''):
bulkradii[k][j] = float(columns[i])
j = j + 1
if (j%33 == 0):
j = 0
k = k + 1
# 密度 [unit: g cm^-3] 定数データ読み込み
# index とカテゴリの対応は粒径と同じ。
bulkdens = [[0] * 33 for i in range(7)]
with open("bulkdens.asc_s_0_03_0_9") as f2:
k = 0
j = 0
for line in f2:
records = line.rstrip('\n')
columns = records.split(' ')[:]
for i in range(len(columns)):
if (columns[i] != ''):
bulkdens[k][j] = float(columns[i])
j = j + 1
if (j%33 == 0):
j = 0
k = k + 1
# 質量 [unit: g] 定数データ読み込み
# index とカテゴリの対応は粒径と同じ。
masses = [[0] * 33 for i in range(7)]
with open("masses.asc") as f3:
k = 0
j = 0
for line in f3:
records = line.rstrip('\n')
columns = records.split(' ')[:]
for i in range(len(columns)):
if (columns[i] != ''):
masses[k][j] = float(columns[i])
j = j + 1
if (j%33 == 0):
j = 0
k = k + 1
# WRF 出力結果を読み込み
ncfile = Dataset("wrfout_d01_0001-01-01_00:50:00")
# 出力結果の cloud and rain bin データを xarray dataset に変換。
vlist = ['ff1i01', 'ff1i02', 'ff1i03', 'ff1i04', 'ff1i05',
'ff1i06', 'ff1i07', 'ff1i08', 'ff1i09', 'ff1i10',
'ff1i11', 'ff1i12', 'ff1i13', 'ff1i14', 'ff1i15',
'ff1i16', 'ff1i17', 'ff1i18', 'ff1i19', 'ff1i20',
'ff1i21', 'ff1i22', 'ff1i23', 'ff1i24', 'ff1i25',
'ff1i26', 'ff1i27', 'ff1i28', 'ff1i29', 'ff1i30',
'ff1i31', 'ff1i32', 'ff1i33']
xdsff1i = getvar(ncfile, "ff1i01")
xdsff1i = xdsff1i.to_dataset()
for ivar in vlist:
xdsff1i[ivar] = getvar(ncfile, ivar)
# 粒径を半径から直径に、単位を cm から mm に、それぞれ変換。
diameter = np.zeros((33), float)
for i in range(0,33):
diameter[i] = bulkradii[0][i] * 2. * 10. # unit: diameter in mm
# 特定グリッドの指定 (水平分布で極大値のあったグリッド)
jj = 22
ii = 19
for kk in [3, 2, 1, 0]:
# 粒径分布データ用の numpy array を初期化。
ff1i = np.zeros((33), float)
# 33 bin に分かれた変数を一つの numpy array に結合
i = 0
for ivar in vlist:
ff1i[i] = xdsff1i[ivar][kk,jj,ii].to_numpy()
i = i + 1
# 粒形分布 N(D) [m^-3 mm^-1] 計算
for i in range(0,33):
# unit: (kg kg^-1) (g^-1) (g cm^-3) (mm^-1)
# -> (kg kg^-1) (kg^-1) (kg m^-3) (mm^-1)
# -> m^-3 mm^-1 (多分これであっているはず)
ff1i[i] = (ff1i[i] / (masses[0][i] * 0.001)) * (bulkdens[0][i] * 1000.) / (diameter[i] * 1000.)
# 粒径分布データ描画。ただし、rain bin のみ。
plt.plot(diameter[16:33], ff1i[16:33], label="k = "+str(kk))
plt.scatter(diameter[16:33], ff1i[16:33])
plt.yscale('log')
plt.xlim(0,6)
plt.ylim(0.01, 10000)
plt.title('N(D) for rain at ('+str(ii)+','+str(jj)+')')
plt.xlabel('Diameter (mm)')
plt.ylabel('Number concentration (mm$^{-1}$ m$^{-3}$)')
plt.grid()
plt.legend()
plt.show()粒形分布を確認すると、地上に近い (i.e., k = 0) ほど粒径 2 mm 未満の頻度が低く、上空 (i.e., k = 3) ほど頻度が高くなっている。一方、粒径 2 mm よりも大きい粒径は地上ほど頻度が高い。また、頻度のピークは、地上に近いほど複数 (粒径 0.26 mm, 0.51 mm, 1.62 mm) 現れる傾向にある。

鉛直分布を確認した時、雨水混合比の値は k = 8 を極大とし、地上に向かって減少していた。これは、粒形分布では第一近似として粒径 2 mm 未満の頻度が低くなっていたことに対応していると考えられる。雨水混合比としては減少する一方、粒径 2 mm 以上の頻度が僅かながら高くなっていた。このことは、雨滴同士の衝突併合によって雨粒が地上に向かって成長している可能性を示唆する。このように、粒形分布を確認することで雨の特徴をより多角的に捉えることが可能となる。
おわりに
今回は、WRF-SBM を用いた粒形分布の解析例を示した。実は、十数年前に WRF モデルの version 3 系列を利用したことがあった。その当時よりも利用可能なオプションが格段に増えており、使い勝手もとてもよくなっていると感じた。特に、描画を Python で行える点は、近年の流行を追っていて舌を巻く。当時は大雨を再現するだけでなく出力結果の解析にも時間と労力を費やしていたが、今後はそんな苦労も少なくなるだろうか。
参考文献
- wrf-model: https://github.com/wrf-model/WRF
- wrf-python: https://github.com/NCAR/wrf-python
- Khain, A. P., A. Pokrovsky, M. Pinsky, A. Seifert, and V. Phillips, 2004: Effects of atmospheric aerosols on deep convective clouds as seen from simulations using a spectral microphysics mixed-phase cumulus cloud model. Part I: Model description. J. Atmos. Sci., 61, 2963–2982.
- Khain, A. P., N. Benmoshe, and A. Pokrovsky, 2008: Factors determining the impact of aerosols on surface precipitation from clouds: An attempt at classification. J. Atmos. Sci., 65, 1721–1748.
- Khain, A. P., D. Rosenfeld, A. Pokrovsky, U. Blahak, and A. Ryzhkov, 2011: The role of CCN in precipitation and hail in a midlatitude storm as seen in simulations using a spectral (bin) microphysics model in a 2D dynamic frame. Atmos. Res., 99, 129–146.
- Igel, A. L., and S. C. van den Heever, 2017: The role of the gamma function shape parameter in determining differences between condensation rates in bin and bulk microphysics schemes. Atmos. Chem. Phys., 17, 4599–4609.
更新履歴
- 2024-01-19: 初稿
- 2024-01-20: 誤字を修正
- 2024-01-23: 表記を修正
- 2024-02-01: Registory の URL を修正
- 2024-05-26: 定数ファイル読み込み時の index とカテゴリの対応表を修正
Miscellaneous — Jan 19, 2024
Made with ❤ and at Japan.