反射強度・反射因子差のバイアス補正

はじめに

気象レーダーによって観測された要素は、そのまま利用するのではなく校正を要する。多くの場合、レーダー設置時や点検の際に校正が行われる。しかしながら、校正が不十分な場合や経年劣化によって、再校正が必要になる場合がある。校正がサイト側で行われるのならば、データの利用者は特に気にしなくて良いだろう。そうではないならば、データの利用者が適切に校正を行うとともにバイアス補正をする必要がある。
といっても真値が分からないので、多くの場合散乱シミュレーションで得た結果との差をバイアスとするようだ (Goddard et al. 1994; 増田 2016)。今回は、主に Goddard et al. (1994) の手法により、データ利用者で行う校正とそれからバイアス補正値の算出について述べる。

方針

• 偏波間位相差変化率 KDP にはバイアスが存在しないことを前提とする。
• 散乱シミュレーションで反射強度・反射因子差・偏波間位相差変化率を算出する。
  • 詳細は、粒径分布とレーダー変数やSelf consistency principleを参照。
• 反射強度・反射因子差のバイアス値を算出する。
  • Goddard et al. (1994) 及び 増田 (2016; 3.2.1, 3.2.2 小節) を参考にした。

反射強度のバイアス補正値算出

まず、散乱シミュレーションで反射強度・反射因子差・偏波間位相差変化率を算出する。Self consistency principleと同様に、Pytmatrix を利用した。帯域はC、温度 10$^{\degree}\rm C$、ガンマ分布の修正パラメータ 5.0、雨滴の縦横比関数 Thurai et al. (2007) とした。
その後、実データの偏波間位相差変化率を用いて反射強度を算出。式は下記。

ここで、添字の obs はレーダー観測値、sim は散乱シミュレーションによる値。$N$は観測データ数。$C_{\rm 1}, C_{\rm 2}$ は散乱シミュレーションにより求めた定数。$C_{\rm 1} = 0.0003, C_{\rm 2} = 0.8$。

バイアスが存在しないと仮定した偏波間位相差変化率を用い、散乱シミュレーションから得た平均的な反射強度と偏波間位相差変化率との自己整合性から反射強度のバイアス補正値を算出する。式は下記。

反射因子差のバイアス補正値算出

反射因子差のバイアス補正値については、後に述べるバイアス補正済の反射強度を用い、算出。式は下記。

ここで、$Z_{\ast} = 10^{Z_{\rm H(obs)} - BIAS_{Z_{\rm H}}}$。添字の obs はレーダー観測値、sim は散乱シミュレーションによる値。$N$は観測データ数。$D_{\rm 1}, D_{\rm 2}$ は散乱シミュレーションにより求めた定数。$D_{\rm 1} = 0.11, D_{\rm 2} = 0.25$。

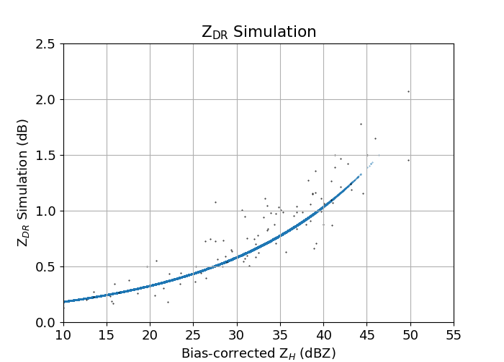
バイアス補正済みの反射強度を用い、反射因子差と反射強度との自己整合性から反射因子差のバイアスを算出する。式は下記。

おわりに

利用者側で行う、反射強度・反射因子差のバイアス補正について述べた。

参考文献

• Goddard, J. W. F., J. Tan, and M. Thurai, 1994: Technique for calibration of meteorological radars using differential phase. Electron. Lett., 30, 166–167. doi:10.1049/el:19940119
• 増田有俊, 2016: Ｘバンド偏波レーダによる積乱雲の構造解析を基礎にした降水セルのライフステージ判別と局地的豪雨予測手法の開発に関する研究. 京都大学学位論文, 121pp. doi:10.14989/doctor.k19691

Miscellaneous — Jan 26, 2022