Self-consistency Principle

はじめに

Self-consistency principle とは、Goddard et al. (1994) で提唱された、水平偏波反射強度 (Z, 以降、反射強度と略す) の校正方法の一つ。雨に対し、$K_{\rm DP}/Z \, = \, Z_{\rm DR}$ の関係から様々な粒径分布をシミュレーションしたものを真値として反射強度の校正をする、というもの。ただし、Goddard et al. (1994) の手法は降雨減衰が考慮されていないため、降雨減衰の影響が無視出来ない X・C バンドレーダーでは利用しにくいという欠点があった。Adachi et al. (2015) ではその欠点を補う、降雨減衰を考慮した校正方法が提案されている。

二重偏波レーダー変数の算出とその補正では、校正済の反射強度が得られていることを前提としていた。降水強度推定に $K_{\rm DP}$ を用いるのであれば、反射強度の校正は必要ないじゃないか、と考えることも出来る。しかしながら、現業レーダーの場合、世界気象機関 (WMO) でレーダー変数のバイアスをある決められた値以下にしましょうという基準 (努力目標に近い) があり、その変数に反射強度も入っているため校正は必須となる。加えて、受信電力の弱い領域では反射強度を用いて降水強度を推定した方が、降水強度の推定精度が総合的に向上する場合が多い。なので、反射強度の校正は、気象レーダーそのものひいては降水強度の量的精度向上にとって必要かつ重要なプロセスなのである。本稿では Self-consistency principle による反射強度の校正について述べる。

実施環境

• 環境構築
• The Python ARM Radar Toolkit (Py-ART)

今回は、こちらの ipython notebook に沿ってシミュレーションを行う。その後、こちらの実データを用い、実際に校正が必要かどうか確認する。

シミュレーション

実施環境で環境構築したものに加え、下記を導入する。

conda install pytmatrix

https://github.com/jleinonen/pytmatrix/wiki

雨滴粒径分布

まず、異なる形状をした雨滴データを用意する。雨滴の縦横比を近似的に求める方法が幾つか提案されていて、pytmatrix に実装されている。

• Thurai et al. (2007)
  • 2D-ビデオ観測で得られた雨滴の形状の近似式から縦横比を算出
• Beard and Chuang (1987)
  • 平衡モデルから縦横比を算出
• Pruppacher and Beard (1970)
  • 風洞実験データから縦横比を算出

図は下記の通り。横軸が雨滴の直径、縦軸が雨滴の縦横比。どの方法でも雨滴の直径が大きくなるにつれて縦横比が概ね小さくなる分布となる。

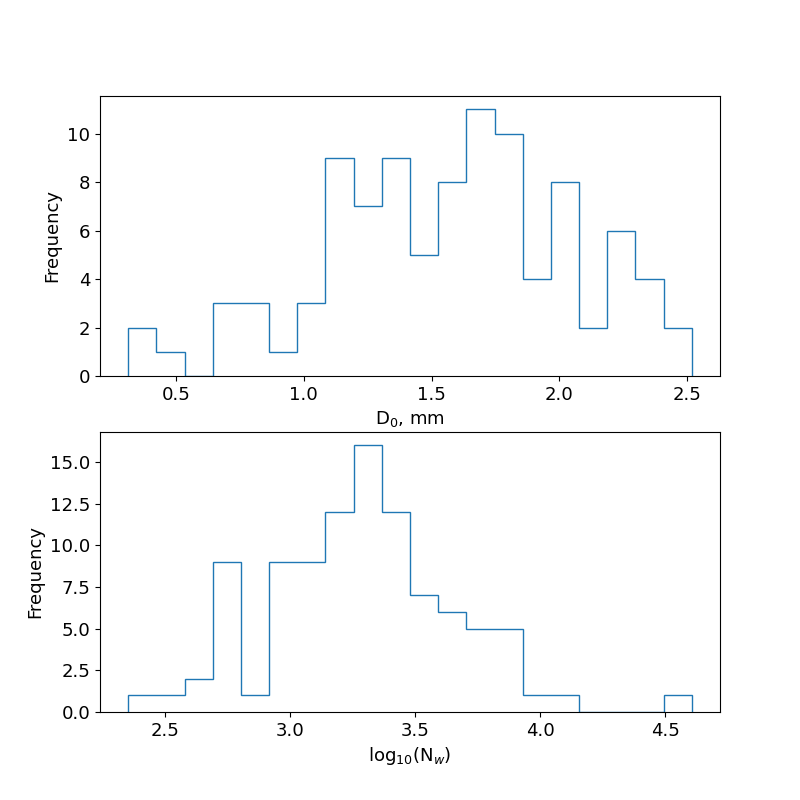
次に、上記で用意した異なる形状をした雨滴データから、雨滴粒径分布 (Drop Size Distribution) を算出する。雨滴粒径分布の推定は、Bringi and Chandrasekar (2001) の式 7.62 に則り規格化したガンマ分布を仮定する。その際、shape parameter ($\mu$)、雨滴の体積直径 ($D_{\rm 0}$)、intercept parameter ($N_{w}$) をそれぞれ与える。上図は $D_{\rm 0}$ の頻度分布、下図は $N_{w}$ の頻度分布。それぞれ、雨滴粒径分布、1立方メートルあたりの密度と解釈できる。ピーク値でみると、$D_{\rm 0}$ 1.7 mm 程度、$N_{w}$ 2000 mm$^{\rm -1}$ m$^{\rm -3}$ 程度なので、層状性の降雨に近い分布である。もう少し値の大きい $D_{\rm 0}$ も含まれているので、対流性のものも混じっているようだ。

レーダー変数推定

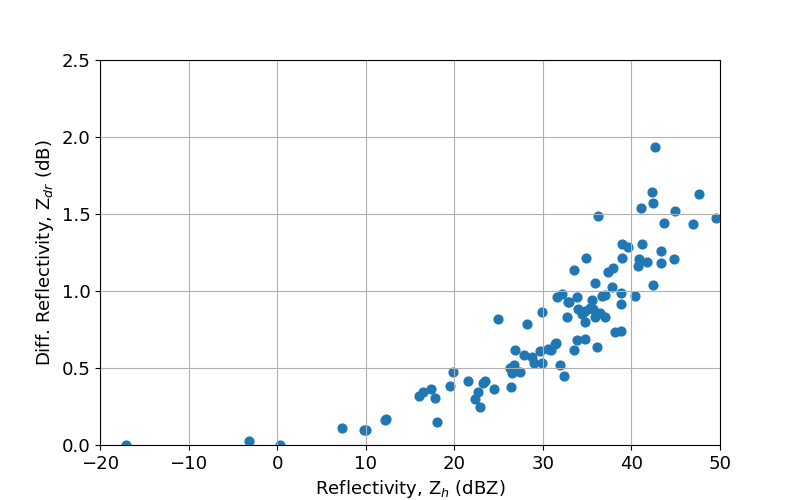
上記で得た雨滴粒径分布から、反射強度・反射因子差・偏波間位相差変化率をそれぞれ求める。確認のため、反射強度と反射因子差の頻度分布を下図に示す。反射強度の値が大きくなるとともに、反射因子差の値が大きくなるような分布をしている。反射強度の大きい雨粒ほど扁平な形状をしているようだ。

$f(K_{\rm DP}/Z) \, = \, Z_{\rm DR}$ 分布

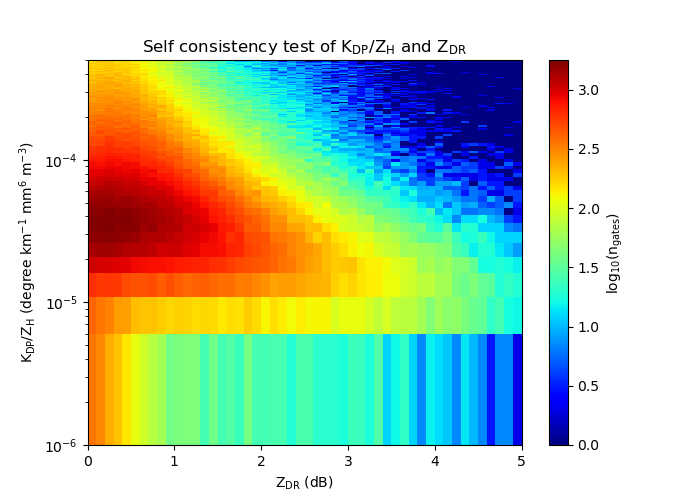
ようやく Self-consistency の関係を確認する準備が整った。横軸に $Z_{\rm DR}$、縦軸に $K_{\rm DP}/Z$ をとり頻度分布を描いたものが下図。0.00007 degree km$^{\rm -1}$ mm$^{\rm -6}$ m$^{\rm 3}$ をピーク値とし、それ以降は $Z_{\rm DR}$ の増加とともにべき乗で減少するような分布をしている。今回は雨滴粒径分布をシミュレーションで算出したけれども、可能であればディスドロメータやビデオ観測等を用いて実際の雨滴粒径分布を得た上で真値を算出すると、より高精度の真値が得られると考えられる。

実例

上記までで、シミュレーションによる真値が得られた。簡単に言うと、この真値とのズレが反射強度のバイアスと考えることが出来る (反射因子差・偏波間位相差変化率がそれぞれ正しく校正されていることが前提)。サンプルデータで反射強度の校正の余地があるかどうか実際に調べてみる。下図は、暖色系ほど頻度が高く寒色系ほど頻度が低くなっている。頻度の高い分布を辿ると、概ね先程確認したシミュレーションの分布に近いところにある。ただし、先程のシミュレーションでは気温が 10$^{\circ}C$ のみを対象としている一方で実例では全ての仰角分を描画している。このため、全てのデータがシミュレーションの分布に乗る訳ではない。正確に行うならば、用いるデータの仰角・高度情報から気温を推定し、条件に一致するデータのみを取り出す必要があるだろう。

おわりに

今回は、Self-consistency principle と銘打って反射強度の校正について扱った。

参考文献

• Adachi, A., T. Kobayashi, H. Yamauchi, 2015: Estimation of raindrop size distribution and rainfall rate from polarimetric radar measurements at attenuating frequency based on the self-consistency principle. J. Meteor. Soc. Japan, 93A, 359–388.
• Beard, K. V., and C. Chuang, 1987: A new model for the equilibrium shape of raindrops. J. Atmos. Sci., 44, 1509–1524.
• Bringi, V. N. and V. Chandrasekar, 2001: Polarimetric Doppler Weather Radar: Principles and Applications. Cambridge University Press, 636 pp.
• Goddard, J. W. F., J. Tan, and M. Thurai, 1994: Technique for calibration of meteorological radars using differential phase. Electron. Lett., 30, 166–167.
• Pruppacher, H. R., and K. V. Beard, 1970: A wind tunnel investigation of the internal circulation and shape of water drops falling at terminal velocity in air. Quart. J. Roy. Meteor. Soc., 96, 247–256.
• Thurai, M., G. J. Huang, V. N. Bringi, W. L. Randeu, and M. Schönhuber, 2007: Drop shapes, model comparisons, and calculations of polarimetric radar parameters in rain. J. Atmos. Oceanic Technol., 24, 1019–1032.

更新履歴

• 2021-09-04: 初稿
• 2021-09-09: 誤字を修正

Miscellaneous — Sep 4, 2021

---

View / Make Comments