Takashi Unuma's blog.

Home About Archive

KDP推定アルゴリズムの比較

はじめに

降水強度のKDP推定アルゴリズムについてでは、主に Reimel and Kumjian (2021) で用いられた偏波間位相差変化率 ( $K_{\rm DP}$ ) 推定アルゴリズムについて概観した。各アルゴリズムの内容が分かってきたので、どのような分布が得られ処理前後でどのように変化するかを実際に手を動かしながら確認してみる。今回は、Py-ART にお世話になった。

比較方法

Py-ART 環境構築: こちら
サンプルデータ: こちら
スクリプト: こちらを参考に下記を作成

下記スクリプトの 10, 12 行目の内、いづれかをコメントアウトし実行する。デフォルトは kdp_maesaka を用いて処理・描画する。

import numpy as np
import matplotlib.pyplot as plt
import pyart

# Read sample data and select sweep id = 0
radar = pyart.io.read_mdv('095636.mdv')
radar = radar.extract_sweeps([0])

# phase_proc_lp
#phidp, kdp = pyart.correct.phase_proc_lp(radar, 0.0, debug=True, LP_solver='cvxopt')
# kdp_maesaka
kdp, phidpf, phidp = pyart.retrieve.kdp_maesaka(radar, gatefilter=None, debug=True)

radar.add_field('corrected_differential_phase', phidp)
radar.add_field('corrected_specific_diff_phase', kdp)

# create a plot of the various differential phase fields
display = pyart.graph.RadarDisplay(radar)
fig = plt.figure(figsize=(10, 10))
ax1 = fig.add_subplot(221)
display.plot('differential_phase', 0, ax=ax1,
             title='Raw Differential Phase', colorbar_label='',
             axislabels_flag=False)
ax2 = fig.add_subplot(222)
display.plot('corrected_differential_phase', 0, ax=ax2,
             title='Processed Differential Phase', colorbar_label='',
             axislabels_flag=False)
ax3 = fig.add_subplot(223)
display.plot('specific_differential_phase', 0, ax=ax3, vmin=0, vmax=6,
             title='Raw Specific Differential Phase', colorbar_label='',
             axislabels_flag=False)
ax4 = fig.add_subplot(224)
display.plot('corrected_specific_diff_phase', 0, ax=ax4, vmin=0, vmax=6,
             title='Processed Specific Differential Phase',
             colorbar_label='',
             axislabels_flag=False)
plt.show()

# plot a fields from a single ray
display = pyart.graph.RadarDisplay(radar)
fig = plt.figure(figsize=[10, 5])
ax = fig.add_subplot(111)
ray_num = 191

# filtered phidp and original phidp
display.plot_ray('corrected_differential_phase', ray_num, format_str='b-',
                 axislabels_flag=False, title_flag=False, ax=ax)
display.plot_ray('differential_phase', ray_num, format_str='g-',
                 axislabels_flag=False, title_flag=False, ax=ax)

# set labels
ax.set_ylim(-200, 200)
ax.set_ylabel('Differential phase shift (degrees)')
ax.set_xlabel('Range (km)')

# plot KDP on second axis
ax2 = ax.twinx()
display.plot_ray('corrected_specific_diff_phase', ray_num, format_str='r-',
                 axislabels_flag=False, title_flag=False, ax=ax2)

ax2.set_ylim(-2, 8)
ax2.yaxis.grid(color='gray', linestyle='dashed')
ax.legend(display.plots,
          ["Filtered phiDP", "Original phiDP", 'KDP'],
          loc='upper right')
plt.show()

結果

今回は PHASE_PROC_LP と KDP_MAESAKA を例に、 PPI 水平分布と ray 方向のグラフとをそれぞれ比較してみる。

PPI 水平分布

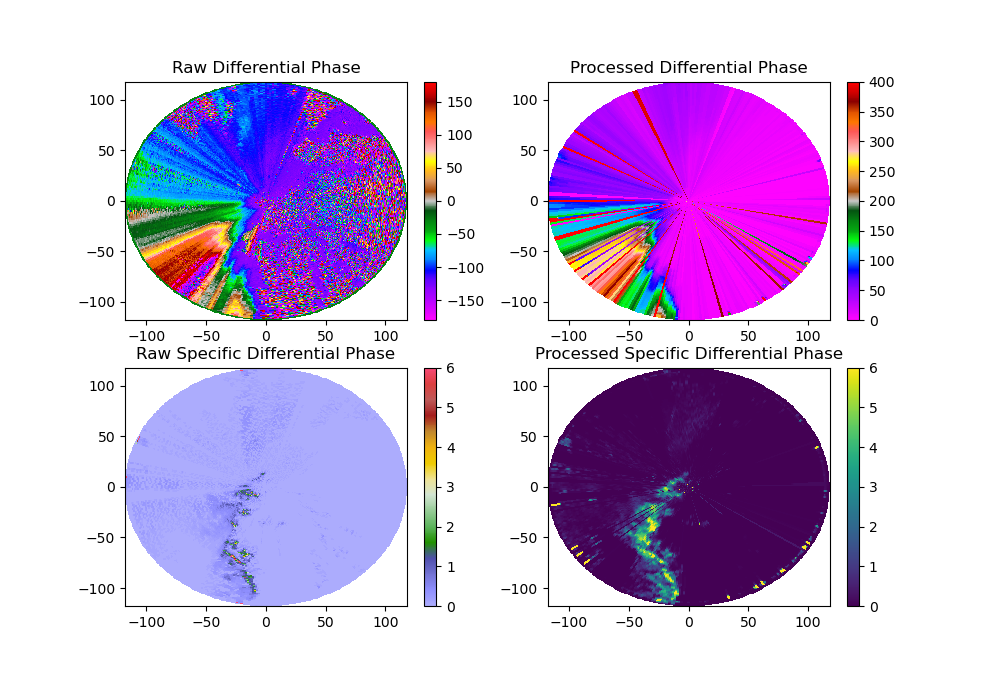
まず、PPI 水平分布を確認する。各図の説明は下記。

左上: 元の $\Phi_{\rm DP}$
右上: 処理済み $\Phi_{\rm DP}$
左下: 元の $K_{\rm DP}$
右下: 処理済み $K_{\rm DP}$

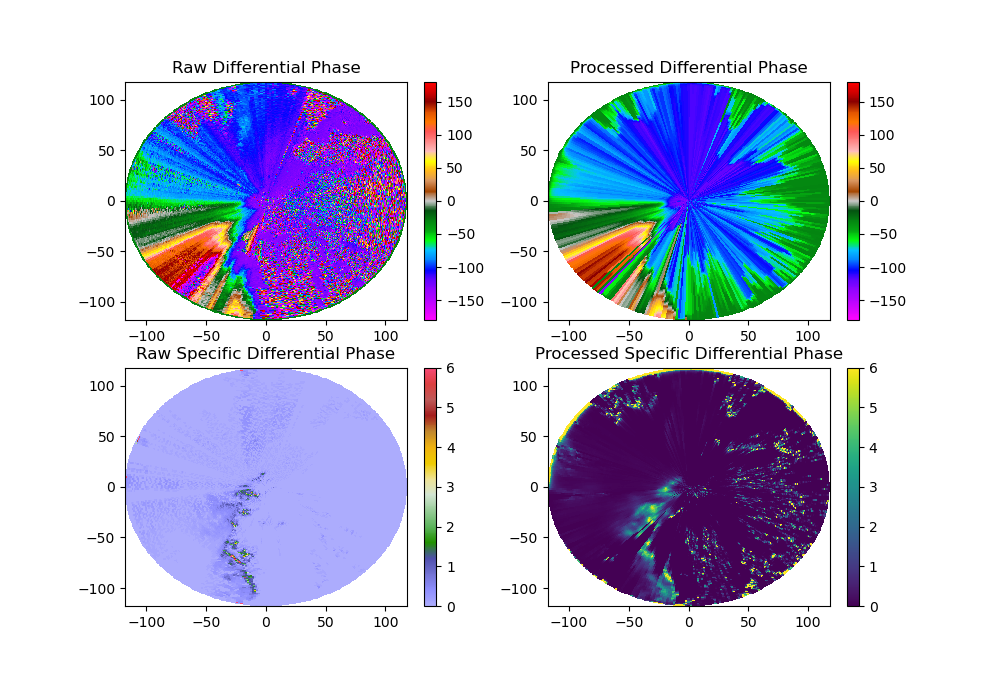
PHASE_PROC_LP の処理済み $\Phi_{\rm DP}$ は元の $\Phi_{\rm DP}$ と比べてかなり平滑化されている。横軸で 0〜100 km の範囲でややまだら模様になっている部分がほぼ 0 degree になっている。一方、KDP_MAESAKA では、処理済み $\Phi_{\rm DP}$ は元データである程度滑らかなところはそのまま利用し、まだら模様になっている部分を落としているようだ (-50 degree 以下の色の階調が緑に変化している部分)。 $K_{\rm DP}$ の分布も $\Phi_{\rm DP}$ の処理具合に依存し、PHASE_PROC_LP の処理済み $K_{\rm DP}$ は KDP_MAESAKA よりも PHASE_PROC_LP で分布としては滑らかに見える。

PHASE_PROC_LP

KDP_MAESAKA

ray 方向のグラフ

次に、ray 方向のグラフを確認する。各実線の説明は下記。

青: 処理済み $\Phi_{\rm DP}$
緑: 元の $\Phi_{\rm DP}$
赤: 処理済み $K_{\rm DP}$

先ほど PPI で確認したように、処理済み $\Phi_{\rm DP}$ はどちらの場合も非常に滑らかな分布となっている (青実線)。値の下限が 0 とそうでない場合になっているけれども、値域の 0〜360 と -180〜180 の違いであるため値の変動を見ることが本質。一方、処理済み $K_{\rm DP}$ (赤実線) を見ると特徴が異なっている。PHASE_PROC_LP の場合は処理済み $\Phi_{\rm DP}$ の勾配に応じた値の変化をしている。KDP_MAESAKA の場合は処理済み $\Phi_{\rm DP}$ が滑らかでも、元の $\Phi_{\rm DP}$ (緑実線) にある細かな勾配も値の変化として表現されている。

PHASE_PROC_LP

KDP_MAESAKA

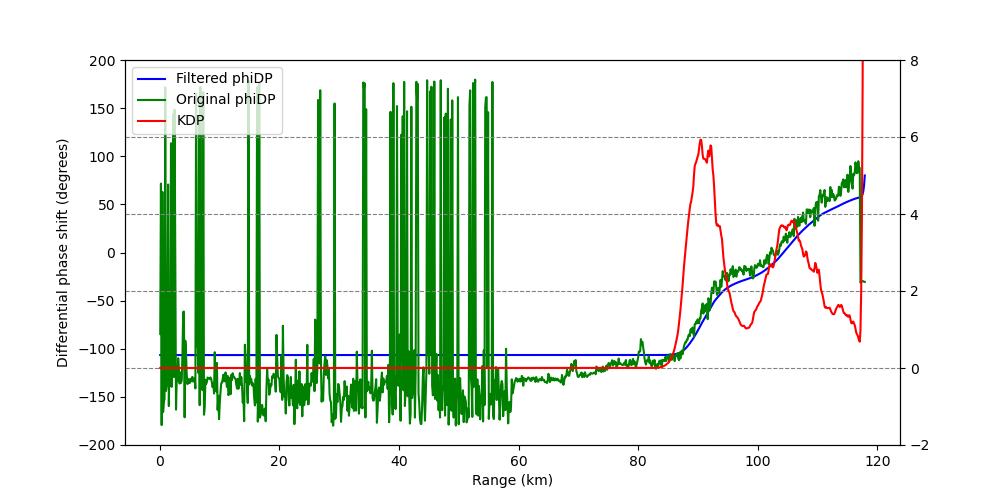
考察

PHASE_PROC_LP では $\Phi_{\rm DP}$ の平滑化処理がかなり強めのようだ。その平滑化済の $\Phi_{\rm DP}$ から有限差分で $K_{\rm DP}$ を計算するため、水平分布・ray 方向のグラフで見ても非常に滑らか分布・値を示しているようだ。滑らかな分布が得られる一方で、局所性を全て棄却しているので $K_{\rm DP}$ の値には必然的に上限ができていそうだ。
KDP_MAESAKA では、フィルターによる平滑化処理というよりはフィルターの重みで平滑化度合いが決まっているようだ。加えて、cost function が最小となるように平滑化した $\Phi_{\rm DP}$ を元の値に近づける。このため、たとえ処理済み $\Phi_{\rm DP}$ で平滑化されていても、元の $\Phi_{\rm DP}$ の変化を反映出来るという訳だ。ただ、元の $\Phi_{\rm DP}$ を適切に処理しておかないと、 $K_{\rm DP}$ 計算時に偽の勾配を表してしまう。KDP_MAESAKA の PPI 水平分布で $K_{\rm DP}$ の値が大きい部分が散在しているのは、こういった部分が反映されているものと考えられる。このように、元の $\Phi_{\rm DP}$ に対するフィルター・平滑化処理のかけ方が重要となるのは、どの推定手法でも共通のようだ。

おわりに

Py-ART のサンプルデータ・サンプルスクリプトを用い、幾つかのKDP推定アルゴリズムについて実際に手を動かしながら確認してみた。図や式を眺めていたときとは異なり、計算時の課題やアルゴリズムの具体的な特徴を把握することが出来た。

参考文献

Reimel, K. J., and M. R. Kumjian, 2021: Evaluation of KDP estimation algorithm performance in rain using a known-truth framework. Journal of Atmospheric and Oceanic Technology, 38, 587–605, doi:10.1175/JTECH-D-20-0060.1.

Miscellaneous — Aug 19, 2021

View / Make Comments

Made with ❤ and at Japan.