Dew Point Temperature

はじめに

大気中の熱力学的要素として、気温・相対湿度といった物理量が存在する。それらだけでなんらかの意味を見出すことも可能であるが、熱力学関数を用いて別の物理量あるいは保存量に変換することで、解釈を容易にすることができうる。雲・降水過程においては、水蒸気が凝結することによって雲を形成し、ひいては降水をもたらす。このため、凝結する温度を的確に把握することは雲・降水過程の理解に重要な役割を果たす。そこで、本稿では露点温度に焦点を当て、その様々な算出方法について概観する。観測データであれば、露点温度を計測している場合もあるものの、近年の測器では水蒸気関連のデータを直接相対湿度として観測している場合もあるようだ。また、数値モデルの出力も気温・相対湿度となっている場合が多く、露点温度を出力している場合は少ないと考えられる。これらの実情を踏まえ、入力データとして気温・相対湿度が与えられていることを前提とする。

露点温度の算出

気温・相対湿度から露点温度を直接算出することは出来ない。下記に示す通り、間接的に幾つかの物理量を介することになる。加えて、それらの物理量算出時に用いる熱力学関数も幾つかの方法が提案されているので、一つずつ述べることとする。大まかな流れは下記となる。

• 気温から飽和水蒸気圧を求める
• 飽和水蒸気圧と相対湿度から水蒸気圧を求める
• 水蒸気圧から露点温度を求める

1つ目の飽和水蒸気圧を求める式が最も重要で、3つ目はその式を逆算したものを用いている。つまり、露点温度の算出過程と言いながら、結局は飽和水蒸気圧の算出過程をどう扱うかという問題に帰着するのである。以下、飽和水蒸気圧の算出について提案されている式を列挙する。その後、それらの精度比較について述べる。

飽和水蒸気圧の算出

Tetens (1930)

ここで、$e_{s}$ 飽和水蒸気圧 (Pa)、$T$ 気温 (degree C) である。

WMO Technical Regulations (1979)

ここで、$e_{s}$ 飽和水蒸気圧 (hPa)、$T$ 気温 (K)、$T_{\rm 1}$ 水の三重点の絶対温度 (K) である。

計算手順: 右辺計算後に $10^{\log_{\rm 10} e_{s}} = e_{s}$ の関係を用い、計算する。また、C の float では桁が足りないので double or long-double を用いる。

Bolton (1980)

ここで、$e_{s}$ 飽和水蒸気圧 (Pa)、$T$ 気温 (degree C) である。

精度比較

飽和水蒸気圧算出

菅原・近藤 (1994) が Lowe (1977) の式・Tetens (1930) の式・Bolton (1980) の式を用いて算出した飽和水蒸気圧について、Smithonial Tables (List, 1966) との差について比較している。結果、0〜30 degree C 程度であればそれぞれの式での相対誤差はほぼ 0% に近い。一方、40 degree C を超えると Bolton (1980) の式、0 degree C 以下では Tetens (1930) の式のそれぞれの相対誤差が増大する。

WMO Technical Regulation (1979) の式を用いて算出した飽和水蒸気圧と Bolton (1980) の式を用いて算出した飽和水蒸気圧との差を調べた。結果、-30〜10 degree C であれば差は最大で 0.02 hPa 程度となる。一方、20 degree C 以上では気温の上昇とともに差が急激に増大した。

露点温度算出

富岡 (1988) が WMO Technical Regulations (1979) と Clausius Clapeyron の式を変形したものとを用いて算出した露点温度の精度を比較している。結果、変形式をそのまま用いるのではなく、最小二乗法によって算出し直した式であれば、-80〜35 degree C で誤差 0.004 degree C 以下となる。

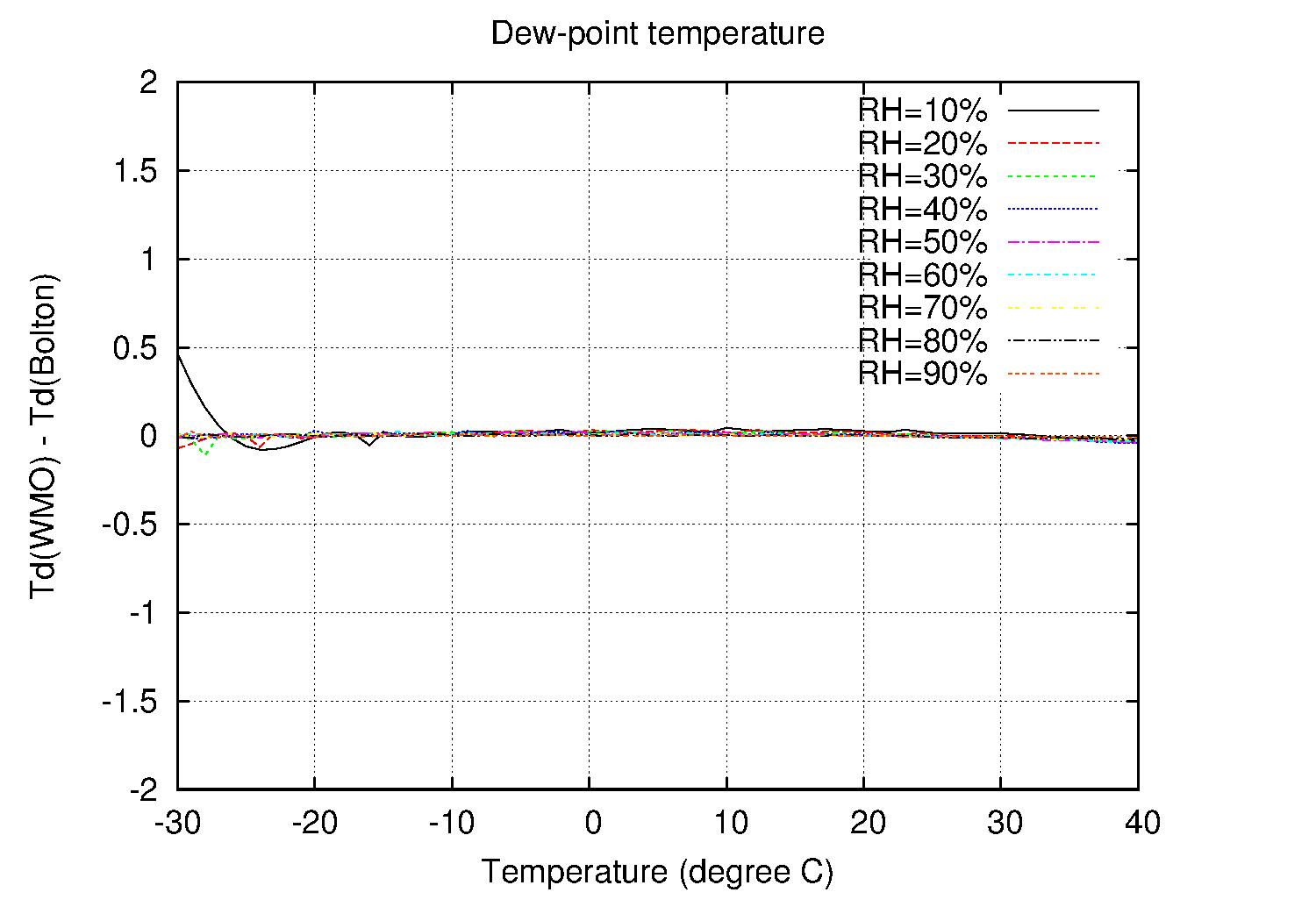
WMO Technical Regulation (1979) の式を用いて算出した露点温度と Bolton (1980) の式を用いて算出した露点温度との差を調べた。結果、-15〜40 degree C であれば相対湿度の値に関わらず 0.05 degree C 未満となった。

結語

与えられる算出式の形態が簡単であるほど計算機での計算効率は良い。ただ、算出式の形態が複雑であるほど精度が高いかと言われると、条件によっては異なるようだ。限定的な範囲での利用 (例えば、気温が 0〜30 degree C の時など) であれば、Bolton (1980) や Tetens (1930) の式を用いても WMO Technical Regulation (1979) とほぼ遜色ない結果が得られるので、問題ない場合が多いだろう。一方、気温や湿度の条件がより多様な状況であれば、精度の担保を得るために WMO Technical Regulation (1979) の式を用いるという手もある思われる。ただし、それは実用上 (計算機資源や表示速度等) の観点を鑑み、利用者が適切なものを選択することになろう。

References

• Bolton, 1980: The Computation of Equivalent Potential Temperature, Monthly Weather Review, 108, 1046-1053.
• 菅原広史, 近藤純正, 1994: 飽和水蒸気圧の計算誤差, 水文・水資源学会誌, 7, 440-443.
  • Tetens (1930), WMO Technical Regulations (1979) の式は、それぞれ菅原・近藤 (1994) より引用した。
• 冨岡四郎, 1988: 水蒸気圧に対応する露点温度の算出法について. 天気, 35, 115-126.

Miscellaneous — Mar 23, 2021